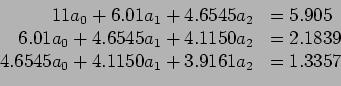Least-Squares Polynomials
- Because polynomials can be readily manipulated, fitting such functions to data that do not plot linearly is common.
- It will turn out that the normal equations are linear for this situation, which is an added advantage.
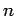 as the degree of the polynomial and N as the number of data pairs. If
as the degree of the polynomial and N as the number of data pairs. If 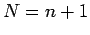 , the polynomial passes exactly through each point and the methods discussed earlier apply, so we will always have
, the polynomial passes exactly through each point and the methods discussed earlier apply, so we will always have 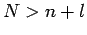 in the following. We assume the functional relationship
in the following. We assume the functional relationship
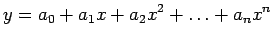 |
(5.5) |
with errors defined by
We again use  to represent the observed or experimental value corresponding to
to represent the observed or experimental value corresponding to 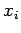 , with
, with 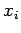 free of error. We minimize the sum of squares;
At the minimum, all the partial derivatives
free of error. We minimize the sum of squares;
At the minimum, all the partial derivatives
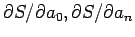 vanish. Writing the equations for these gives
vanish. Writing the equations for these gives 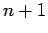 equations:
Dividing each by
equations:
Dividing each by 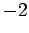 and rearranging gives the
and rearranging gives the 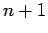 normal equations to be solved simultaneously:
normal equations to be solved simultaneously:
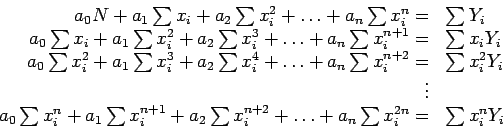 |
(5.6) |
Putting these equations in matrix form shows the coefficient matrix;
![\begin{displaymath}\left[
\begin{array}{rrrrrl}
N & \sum x_i & \sum x_i^2 & \sum...
...sum x_i^2Y_i\\
\vdots \\
\sum x_i^n Y_i\\
\end{array}\right]\end{displaymath}](img734.png) |
|
|
(5.7) |
All the summatins in Eqs. 5.6 and 5.7 run from 1 to 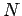 . We will let B stand for the coefficient matrix.
. We will let B stand for the coefficient matrix.
- Equation 5.7 represents a linear system. However, you need to know that this system is ill-conditioned and round-off errors can distort the solution: the
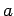 's of Eq. 5.5. Up to degree-3 or -4, the problem is not too great. Special methods that use orthogonal polynomials are a remedy. Degrees higher than 4 are used very infrequently. It is often better to fit a series of lower-degree polynomials to subsets of the data.
's of Eq. 5.5. Up to degree-3 or -4, the problem is not too great. Special methods that use orthogonal polynomials are a remedy. Degrees higher than 4 are used very infrequently. It is often better to fit a series of lower-degree polynomials to subsets of the data.
- Matrix
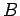 of Eq. 5.7 is called the normal matrix for the least-squares problem. There is another matrix that corresponds to this, called the design matrix. It is of the form;
of Eq. 5.7 is called the normal matrix for the least-squares problem. There is another matrix that corresponds to this, called the design matrix. It is of the form;
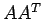 is just the coefficient matrix of Eq. 5.7. It is easy to see that
is just the coefficient matrix of Eq. 5.7. It is easy to see that 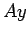 , where
, where 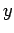 is the column vector of
is the column vector of 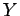 -values, gives the right-hand side of Eq. 5.7. We can rewrite Eq. 5.7 in matrix form, as
-values, gives the right-hand side of Eq. 5.7. We can rewrite Eq. 5.7 in matrix form, as
- It is illustrated the use of Eqs. 5.6 to fit a quadratic to the data of Table 5.4. Figure 5.7 shows a plot of the data. The data are actually a perturbation of the relation
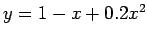 .
.
Table 5.4:
Data to illustrate curve fitting.
![\begin{table}\begin{center}
\includegraphics[scale=1]{figures/3.9.ps}
\end{center}
\end{table}](img740.png) |
Figure 5.7:
Figure for the data to illustrate curve fitting.
|
|
To set up the normal equations, we need the sums tabulated in Table 5.4. The equations to be solved are:
The result is
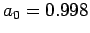 ,
,
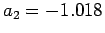 ,
,
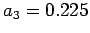 , so the least- squares method gives
which we compare to
, so the least- squares method gives
which we compare to
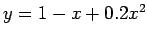 . Errors in the data cause the equations to differ.
. Errors in the data cause the equations to differ.
2004-12-28
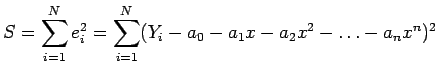
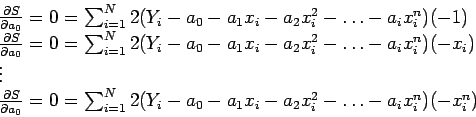
![\begin{displaymath}
A=\left[
\begin{array}{rrrrr}
1 & 1 & 1 & 1 & 1 \\
x_1 & ...
... x_1^n & x_2^n & x_3^n & \ldots & x_N^n\\
\end{array} \right]
\end{displaymath}](img735.png)