Next: Approximation of Functions Up: Interpolation and Curve Fitting Previous: Use of Orthogonal Polynomials Contents
x =(0:0.1:5)'; % x from 0 to 5 in steps of 0.1 y = sin(x); % get y values p = polyfit(x,y,3); % fit a cubic to the data f = polyval(p,x); % evaluate the cubic on the x data plot(x,y,'o',x,f,'-') % plot y and its approximation fSolution:
>> x =(0:0.1:5)'; >> y = sin(x); >> p = polyfit(x,y,3) p = 0.0919 -0.8728 1.8936 -0.1880 >> f = polyval(p,x); >> plot(x,y,'o',x,f,'-');

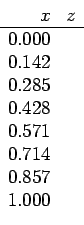
>> Y=[1.5 1.495 1.04 0.821 1.003 0.821 0.442 0.552]'
Y =
1.5000
1.4950
1.0400
0.8210
1.0030
0.8210
0.4420
0.5520
>> z=log(Y)
z =
0.4055
0.4021
0.0392
-0.1972
0.0030
-0.1972
-0.8164
-0.5942

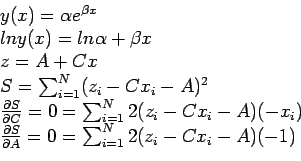
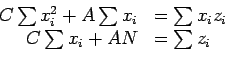
>> x=[0 0.142 0.285 0.428 0.571 0.714 0.857 1]';
>> Y=[1.5 1.495 1.04 0.821 1.003 0.821 0.442 0.552]';
>> z=log(Y);
>> sum(x'*x)
ans = 2.8549
>> sum(x')
ans = 3.9970
>> sum(x'*z)
ans = -1.4491
>> sum(z')
ans = -0.9553
>> A=[ 2.8549 3.997; 3.997 8]
A =
2.8549 3.9970
3.9970 8.0000
>> B=[-1.4491 -0.9553]'
B =
-1.4491
-0.9553
>> X=uptrbk(A,B)
X =
-1.1328
0.4466
so; we obtained >> exp(0.4466) ans = 1.5630we have
>> y=1.5630*exp(-1.1328*x)
y =
1.5630
1.3308
1.1317
0.9625
0.8185
0.6961
0.5920
0.5035
>> plot(x,Y,'o',x,y,'-')
>> x=[0 0.142 0.285 0.428 0.571 0.714 0.857 1]';
>> Y=[1.5 1.495 1.04 0.821 1.003 0.821 0.442 0.552]';
>> p = polyfit(x,Y,3)
p = -0.3476 0.9902 -1.6946 1.5518
>> f = polyval(p,x)
f =
1.5518
1.3301
1.1412
0.9806
0.8423
0.7201
0.6080
0.4998
>> plot(x,Y,'o',x,f,'-');
>> plot(x,Y,'o',x,f,'-',x,y,'+')