Next: Fourier Series Up: Approximation of Functions Previous: Chebyshev Series Contents
function T=Tch(n)
if n==0
disp('1')
elseif n==1
disp('x')
else
t0='1';
t1='x';
for i=2:n
T=symop('2*x','*',t1,'-',t0);
t0=t1;
t1=T;
end
end
save with the name Tch.m. Then;
>>Tch(5) ans =2*x*(2*x*(2*x*(2*x^2-1)-x)-2*x^2+1)-2*x*(2*x^2-1)+x >>collect(ans) ans= 16*x^5-20*x^3+5*xFor Matlab7 users,
function s = symop(varargin);
%SYMOP Obsolete Symbolic Toolbox function.
% SYMOP takes any number of arguments, including %'+','-','*','/','^',
% '(' and ')', concatenates them and symbolically evaluates the %result.
% Copyright (c) 1993-98 by The MathWorks, Inc.
% $Revision: 1.2 $ $Date: 1997/11/29 01:06:41 $
s = [];
for k = 1:nargin
v = varargin{k};
if ~ischar(v), v = char(sym(v)); end
switch v
case {'+','-','*','/','^','(',')'}
s = [s v];
otherwise
s = [s 'sym(''' v ''')'];
end
end
s = eval(s);
>> syms x >> ts=taylor(exp(x),8) ts =1+x+1/2*x^2+1/6*x^3+1/24*x^4+1/120*x^5+1/720*x^6+1/5040*x^7 >> cs=collect(Tch(7)) cs = 64*x^7-112*x^5+56*x^3-7*x >> es=ts-cs/factorial(7)/2^6 es = 1+46081/46080*x+1/2*x^2+959/5760*x^3+1/24*x^4+5/576*x^5+1/720*x^6 >> vpa(es,7) ans = 1.+1.000022*x+.5000000*x^2+.1664931*x^3+.4166667e-1*x^4 +.8680556e-2*x^5+.1388889e-2*x^6
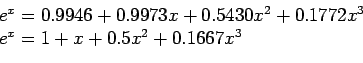
function week8lsgitem3(ll,ul,s)
format short;
%format long;
disp(' x e^x Chebyshev Error Maclaurin Error')
x =(ll:s:ul)';
taylor=exp(x);
max=(ul-ll)/s+1;
for i=1:max
chebyshev=(0.9946 + 0.9973*x(i) + 0.5430*x(i)^2 + 0.1772*x(i)^3);
errorchebyshev(i)=taylor(i)-chebyshev;
maclaurin=(1+x(i)+0.5*x(i)^2+0.1667*x(i)^3);
errormaclaurin(i)=taylor(i)- maclaurin;
D=[x(i),taylor(i),chebyshev,errorchebyshev(i),maclaurin,errormaclaurin(i)];
disp(D);
end
plot(x,errorchebyshev,'o',x,errormaclaurin,'-')
save with the name week8lsgitem3.m. Then;
>> week8lsgitem3(-1,1,0.1)
x e^x Chebyshev Error Maclaurin Error
-1.0000 0.3679 0.3631 0.0048 0.3333 0.0346
-0.9000 0.4066 0.4077 -0.0011 0.3835 0.0231
-0.8000 0.4493 0.4536 -0.0042 0.4346 0.0147
-0.7000 0.4966 0.5018 -0.0052 0.4878 0.0088
-0.6000 0.5488 0.5534 -0.0046 0.5440 0.0048
-0.5000 0.6065 0.6096 -0.0030 0.6042 0.0024
-0.4000 0.6703 0.6712 -0.0009 0.6693 0.0010
-0.3000 0.7408 0.7395 0.0013 0.7405 0.0003
-0.2000 0.8187 0.8154 0.0033 0.8187 0.0001
-0.1000 0.9048 0.9001 0.0047 0.9048 0.0000
0 1.0000 0.9946 0.0054 1.0000 0
0.1000 1.1052 1.0999 0.0052 1.1052 0.0000
0.2000 1.2214 1.2172 0.0042 1.2213 0.0001
0.3000 1.3499 1.3474 0.0024 1.3495 0.0004
0.4000 1.4918 1.4917 0.0001 1.4907 0.0012
0.5000 1.6487 1.6511 -0.0024 1.6458 0.0029
0.6000 1.8221 1.8267 -0.0046 1.8160 0.0061
0.7000 2.0138 2.0196 -0.0058 2.0022 0.0116
0.8000 2.2255 2.2307 -0.0051 2.2054 0.0202
0.9000 2.4596 2.4612 -0.0016 2.4265 0.0331
1.0000 2.7183 2.7121 0.0062 2.6667 0.0516