Interval Halving (Bisection)
- Interval halving (bisection), an ancient but effective method for finding a zero of
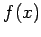 .
.
- It begins with two values for
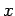 that bracket a
root.
that bracket a
root.
- The function
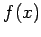 changes signs at these two x-values and, if
changes signs at these two x-values and, if 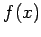 is continuous, there must be at least one root between the values.
is continuous, there must be at least one root between the values.
- A plot of
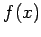 is useful to know where to start.
is useful to know where to start.
- The bisection method then successively divides the initial interval in half, finds in which half the root(s) must lie, and repeats with the
endpoints of the smaller interval.
- The test to see that
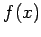 does change sign between points
does change sign between points 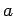 and
and 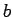 is to see if
is to see if 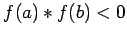 .
.
Look at to the plot of the function (see Fig. 1) to learn where the function crosses the x-axis. MATLAB can do it for us:
>> f = inline ( ' 3 *x + sin ( x) - exp ( x) ')
>> fplot ( f, [ 0 2 ]) ; grid on
And we see from the figure that indicates there are zeros at about 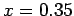 and
and 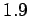 .
.
An algorithm for Halving the Interval (Bisection):

- Think about the multiplication factor, 2
- The final Value of
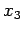 approximates the root, and it is in error by not more than
approximates the root, and it is in error by not more than 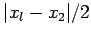 .
.
- The method may produce a false root if
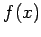 is discontinuous on
is discontinuous on ![$[x_1,x_2]$](img25.png) .
.
To obtain the true value for the root, which is needed to compute the actual error. MATLAB surely used a more advanced method than bisection.
>> solve('3*x + sin(x) - exp(x)')
ans=
.36042170296032440136932951583028
Figure 1:
Plot of the function:
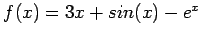
|
|
Table 1:
The bisection method for
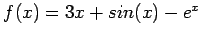 , starting from
, starting from 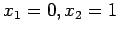 , using a tolerance value of 1E-4.
, using a tolerance value of 1E-4.
![\begin{table}
\begin{center}
\includegraphics[scale=1]{figures/1.2.ps}
\end{center}\end{table}](img27.png) |
2004-10-15

