Some Special Matrices and Their Properties
- Square matrices are particularly important when a system of equations is to be solved. Square matrices have some special properties.
- The elements on the main diagonal are those from the upper-left corner to the lower-right corner. (diagonal elements, diagonal)
- If the nonzero elements of a diagonal matrix all are equal to one, the matrix is called the identity matrix of order n where n equals the number of row and columns. The order-4 identity matrix is
- An important property of an identity matrix, I, is that for any
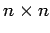 matrix, A,
matrix, A,
- If two rows of an identity, matrix are interchanged, it is called a transposition matrix. (We also get a transposition matrix by interchanging two columns.
- If transposition matrix
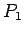 , is multiplied with a square matrix of the same size, A, the product
, is multiplied with a square matrix of the same size, A, the product 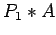 will be the A matrix but with the same two rows interchanged. i.e.:
will be the A matrix but with the same two rows interchanged. i.e.:
- However, if the two matrices are multiplied in reverse order,
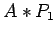 , the result will be matrix A but with the columns of A interchanged.
, the result will be matrix A but with the columns of A interchanged.
- A permutation matrix is obtained by multiplying several transposition matrices.
- A square matrix is called a symmetric matrix when the pairs of elements in similar positions across the diagonal are equal.
- The transpose of a matrix is the matrix obtained by writing the rows as columns or by writing the columns as rows. (A matrix does not have to be square to have a transpose.) The symbol for the transpose of matrix
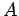 is
is 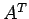 .
.
- It should be clear that
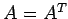 if
if  is symmetric, and that for any matrix, the transpose of the transpose,
is symmetric, and that for any matrix, the transpose of the transpose, 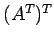 , is just
, is just 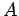 itself. It is also true that
itself. It is also true that
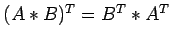 .
.
- When a matrix is square, a quantity called its trace is defined. The trace of a square matrix is the sum of the elements on its main diagonal. The trace remains the same if a square matrix is transposed.
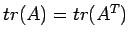
- If all the elements above the diagonal are zero, a matrix is called lower-triangular; it is called upper-triangular when all the elements below the diagonal are zero.
- Tridiagonal matrices are those that have nonzero elements only on the diagonal and in the positions adjacent to the diagonal;
For a tridiagonal matrix, only the nonzero values need to be recorded, and that means that the 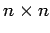 matrix can be compressed into a matrix of 3 columns and n rows.
matrix can be compressed into a matrix of 3 columns and n rows.
- In some important applied problems, only a few of the elements are nonzero. Such a matrix is termed a sparse matrix and procedures that take advantage of this sparseness are of value.
- Division of matrices is not defined, but we will discuss the inverse of a matrix later in
- The determinant of a square matrix is a number. For a
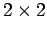 matrix, the determinant is computed by subtracting the product of the elements on the minor diagonal (from upper right to lower left) from the product of terms on the major diagonal.
matrix, the determinant is computed by subtracting the product of the elements on the minor diagonal (from upper right to lower left) from the product of terms on the major diagonal.
- We expand each of the determinants of the minor until we reach
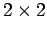 matrices.
matrices.
- In computing the determinant, the expansion can be about the elements of any row or column. To get the signs, give the first term a plus sign if the sum of its column number and row number is even; give it a minus if the sum is odd, with alternating signs thereafter.
- This method of calculating determinants is a lot of work if the matrix is of large size. Methods that triangularize a matrix, as described in Section 1.2, are much better ways to get the determinant.
- If a matrix, B, is triangular (either upper or lower), its determinant is just the product of the diagonal elements:
It is easy to show this if the determinant of the triangular matrix is expanded by minors.
- Determinants can be used to obtain the characteristic polynomial and the eigenvalues of a matrix, which are the roots of that polynomial. (Eigenvalue is a German word, the corresponding English term is characteristic value, but it is less frequently used.)
- The two terms, eigenvalue and characteristic polynomial are interrelated; For matrix
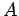 ,
,
 .
.
- The characteristic polynomial is always of degree
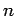 if
if 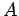 is
is 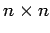 . If we set the characteristic polynomial to zero and solve for the roots, we get the eigenvalues of A. For this example, these are
. If we set the characteristic polynomial to zero and solve for the roots, we get the eigenvalues of A. For this example, these are
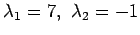 , or, in more symbolic mathematical notation:
, or, in more symbolic mathematical notation:
- We also mention the notion of an eigenvector corresponding to an eigenvalue.
In the current example, the eigenvectors are
- Observe that the trace of A is equal to the sum of the eigenvalues:
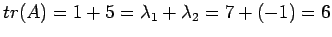 This is true for any matrix: The sum of its eigenvalues equals its trace.
This is true for any matrix: The sum of its eigenvalues equals its trace.
- If a matrix is triangular, its eigenvalues are equal to the diagonal elements. This follows from the fact that its determinant is just the product of the diagonal elements and its characteristic polynomial is the product of the terms
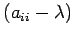 with
with 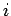 going from
going from 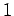 to
to 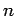 , the number of rows of the matrix.
, the number of rows of the matrix.
whose roots are clearly 1, 4, and 6. It does not matter if the matrix is upper- or lower-triangular.
2004-11-03
![\begin{displaymath}
I_4=
\left[
\begin{array}{cccc}
1 & 0 & 0& 0 \\
0 & 1 & 0& 0 \\
0 & 0 & 1& 0 \\
0 & 0 & 0& 1 \\
\end{array} \right]
\end{displaymath}](img22.png)
![\begin{displaymath}
P_1=
\left[
\begin{array}{cccc}
1 & 0 & 0& 0 \\
0 & 0 & 0...
...8 \\
0 & 7 & 1& 9 \\
4 & 2 & 8&11 \\
\end{array} \right],
\end{displaymath}](img27.png)
![\begin{displaymath}
\left[
\begin{array}{ccc}
1 & x & y \\
x & 2 & z \\
y & z & 3 \\
\end{array} \right]
\end{displaymath}](img29.png)
![\begin{displaymath}
A=
\left[
\begin{array}{rrr}
3 & -1& 4 \\
0 & 2 & 3 \\
...
...& 0& 1 \\
-1 & 2 & 1 \\
4 & -3& 2 \\
\end{array} \right],
\end{displaymath}](img32.png)
![\begin{displaymath}
L=
\left[
\begin{array}{ccc}
x & 0 & 0 \\
x & x & 0 \\
...
... x & x& x \\
0 & x& x \\
0 & 0 & x \\
\end{array} \right]
\end{displaymath}](img37.png)
![\begin{displaymath}
\left[
\begin{array}{ccccc}
x & x & 0 &0 &0 \\
x & x & x ...
... 0 & 0 & x &x &x \\
0 & 0 & 0 &x &x \\
\end{array} \right]
\end{displaymath}](img38.png)
![\begin{displaymath}
\left[
\begin{array}{rr}
-5 & 3\\
7 & 2\\
\end{array} \right], det(A)=(-5)(2)-(7)(3)=-31
\end{displaymath}](img40.png)
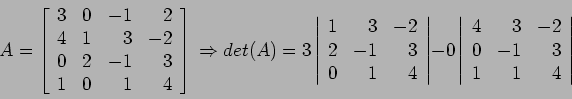
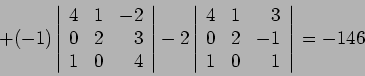
![\begin{displaymath}
det\left[
\begin{array}{rrr}
4 & 0 & 0 \\
6 &-2 & 0 \\
1 &-3 & 5 \\
\end{array} \right]=-40
\end{displaymath}](img44.png)
![\begin{displaymath}
A=\left[
\begin{array}{cc}
1& 3 \\
4 &5 \\
\end{array} \right]
\end{displaymath}](img46.png)
![\begin{displaymath}
P_A(\lambda)=\left\vert A - \lambda I\right\vert=det\left[
\...
...\
4 &5 - \lambda \\
\end{array}\right]=\lambda^2-6\lambda-7
\end{displaymath}](img47.png)
![\begin{displaymath}
w_1=\left[
\begin{array}{c}
1 \\
2 \\
\end{array} \right], w_2=\left[
\begin{array}{r}
-3 \\
2 \\
\end{array} \right]
\end{displaymath}](img52.png)
![\begin{displaymath}
A=\left[
\begin{array}{ccc}
1 & 2 & 3 \\
0 & 4 & 5 \\
0 & 0 & 6 \\
\end{array} \right],
\end{displaymath}](img57.png)
![\begin{displaymath}
det(A-\lambda I)=det\left[
\begin{array}{ccc}
1-\lambda & 2...
...mbda \\
\end{array} \right]=(1-\lambda)(4-\lambda)(6-\lambda)
\end{displaymath}](img58.png)