Nonlinear Data

• In many cases, data from experimental tests are not linear, so we need to fit to them some function other than a first-degree polynomial. Popular forms are the exponential form
  
  $$y=ax^b$$
  
  
  or
  
  $$y =ae^{bx}$$
  
  

• We can develop normal equations to the preceding development for a least-squares line by setting the partial derivatives equal to zero. Such nonlinear simultaneous equations are much more difficult to solve than linear equations. Thus, the exponential forms are usually linearized by taking logarithms before determining the parameters:
  
  $$ln y = ln a + b ln x$$
  
  
  or
  
  $$ln y = ln a + bx$$
  
  
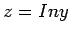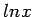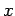  We now fit the new variable $z= In y$ as a linear function of $ln x$ or $x$ as described earlier. Here we do not minimize the sum of squares of the deviations of 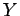$Y$ from the curve, but rather the deviations of $ln Y$.
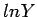  • In effect, this amounts to minimizing the squares of the percentage errors, which itself may be a desirable feature.
  • An added advantage of the linearized forms is that plots of the data on either log-log or semilog graph paper show at a glance whether these forms are suitable, by whether a straight line represents the data when so plotted.
• In cases when such linearization of the function is not desirable, or when no method of linearization can be discovered, graphical methods are frequently used; one merely plots the experimental values and sketches in a curve that seems to fit well.
• Transformation of the variables to give near linearity, such as by plotting against 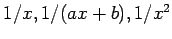$1/x, 1/(ax + b), 1/x^2$, and other polynomial forms of the argument may give curves with gentle enough changes in slope to allow a smooth curve to be drawn. S-shaped curves are not easy to linearize; the relation
  
  $$y= ab^{c^x}$$
  
  
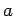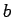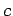  is sometimes employed. The constants $a$, $b$, and $c$ are determined by special procedures. Another relation that fits data to an S-shaped curve is
  
  $$\frac{1}{y}= a + be{-x}$$
  
  
  In awkward cases, subdividing the region of interest into subregions with a piecewise fit in the subregions can be used.