Approximation of Functions

• To get the value of 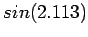$sin(2.113)$ or $e^{-3.5}$
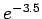
• It doesn't look these up in tables and interpolate! The computer approximates every function from some polynomial that is tailored to give the values very accurately.
• We want the approximation to be efficient in that it obtains the values with the smallest error in the least number of arithmetic operations.
• A second topic, representing a function with a series of sine and cosine terms. A Fourier series, is usually the best way to represent a periodic function, something that cannot be done with a polynomial or a Taylor series. A Fourier series can even approximate functions with discontinuities and discontinuous derivatives.
  • Chebyshev Polynomials and Chebyshev Series: Chebyshev polynomials are orthogonal polynomials that are the basis for fitting nonalgebraic functions with maximum efficiency. They can be used to modify a Taylor series so that there is greater efficiency. A series of such polynomials converges more rapidly than a Taylor series.
  • Fourier Series: These are series of sine and cosine terms that can be used to approximate a function within a given interval very closely, even functions with discontinuities. Fourier series are important in many areas, particularly in getting an analytical solution to partial-differential equations.