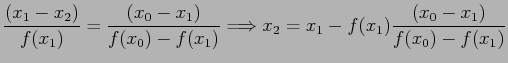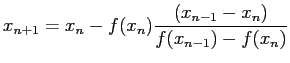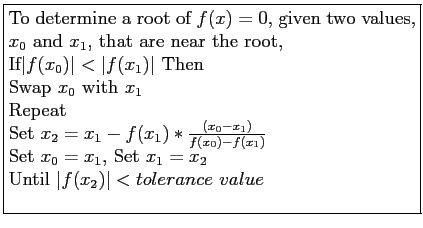- Bisection is simple to understand but it is not the most efficient way to find where
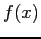 is zero.
is zero.
- Most functions can be approximated by a straight line over a small interval.
Figure 3.4:
Graphical illustration of the Secant Method.
|
|
- The secant method begins by finding two points on the curve of
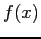 , hopefully near to the root.
, hopefully near to the root.
- As Figure 3.4 illustrates, we draw the line through these two points and find where it intersects the x-axis.
- If
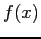 were truly linear, the straight line would intersect the x-axis at the root.
were truly linear, the straight line would intersect the x-axis at the root.
- The intersection of the line with the x-axis is not at
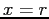 (root) but it should be close to it.
(root) but it should be close to it.
- From the obvious similar triangles we can write
- Because f(x) is not exactly linear,
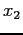 is not equal to
is not equal to 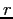 ,
,
- but it should be closer than either of the two points we began with. If we repeat this, we have:
- The net effect of this rule is to set
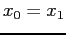 and
and 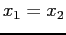 , after each iteration.
, after each iteration.
- The technique we have described is known as, the secant method because the line through two points on the curve is called the secant line.
- An algorithm for the Secant Method:
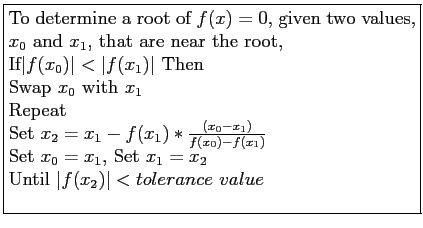
Table 3.2:
The Secant method for
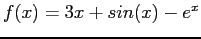 , starting from
, starting from
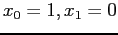 , using a tolerance value of 1E-6.
, using a tolerance value of 1E-6.
![\begin{table}
\begin{center}
\includegraphics[scale=0.6,angle=0.5]{figures/1-10}
\end{center}\end{table}](img256.png) |
- Table 3.2 shows the results from the secant method for the same function that was used to illustrate bisection.
- An alternative stopping criterion for the secant method is when the pair of points being used are sufficiently close together.
- If the method is being carried out by a program that displays the successive iterates, the user can interrupt the program should such improvident behavior be observed.
- If
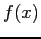 is not continuous, the method may fail.
is not continuous, the method may fail.
- If the function is far from linear near the root, the successive iterates can fly off to points far from the root, as seen if Fig. 3.5.
Figure 3.5:
A pathological case for the secant method.
|
|
- If the function was plotted before starting the method, it is unlikely that the problem will be encountered, because a better starting value would be used.
Cem Ozdogan
2011-12-27