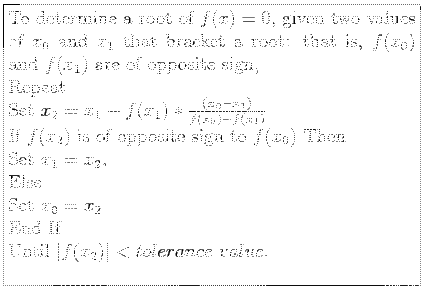- A way to avoid such pathology is to ensure that the root is bracketed between the two starting values and remains between the successive pairs.
- When this is done, the method is known as linear interpolation (regula falsi).
- This technique is similar to bisection except the next iterate is taken at the intersection of a line between the pair of x-values and the x-axis rather than at the midpoint.
- Doing so gives faster convergence than does bisection, but at the expense of a more complicated algorithm.
- An algorithm for the method of false position:
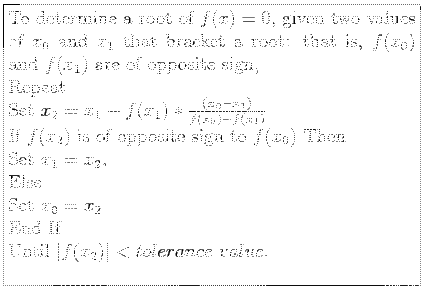
- If
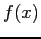 is not continuous, the method may fail.
is not continuous, the method may fail.
Table 3.3:
Comparison of methods,
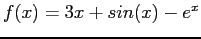 , starting from
, starting from
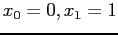 .
.
![\begin{table}
\begin{center}
\includegraphics[scale=0.6]{figures/1-12}
\end{center}\end{table}](img259.png) |
- Table 3.3 compares the results of three methods-interval halving (bisection), linear interpolation, and the secant method for
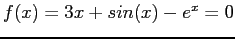
- Observe that the speed of convergence is best for the secant method, poorest for interval halving, and intermediate for false position.
Cem Ozdogan
2011-12-27