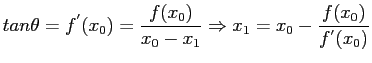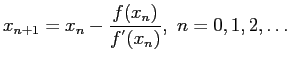Figure 3.6:
Graphical illustration of the Newton's Method.
|
|
One of the most widely used methods of solving equations is Newton's method (Newton did not publish an extensive discussion of this method, but he solved a cubic polynomial in Principia (1687)).
- The version given here is considerably improved over his original example.
- Like the previous ones, this method is also based on a linear approximation of the function, but does so using a tangent to the curve (see Figure 3.6).
- Starting from a single initial estimate,
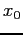 , that is not too far from a root, we move along the tangent to its intersection with the x-axis, and take that as the next approximation.
, that is not too far from a root, we move along the tangent to its intersection with the x-axis, and take that as the next approximation.
- This is continued until either the successive x-values are sufficiently close or the value of the function is sufficiently near zero.
- The calculation scheme follows immediately from the right triangle shown in Fig. 3.6.
and the general term is:
Cem Ozdogan
2011-12-27