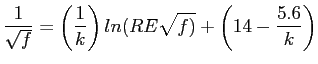Solving Nonlinear Equations

• solve ``$f(x) = 0$''
  • where $f(x)$ is a function of $x$.
  • The values of $x$ that make $f(x) = 0$ are called the roots of the equation.
  • They are also called the zeros of $f(x)$.
• The following non-linear equation can compute the friction factor,$f$:
  $$\frac{1}{\sqrt{f}}=\left(\frac{1}{k}\right)ln(RE\sqrt{f)}+\left(14-\frac{5.6}{k}\right)$$

• The equation for $f$ is not solvable except by the numerical procedures.

1. Interval Halving (Bisection). Describes a method that is very simple and foolproof but is not very efficient. We examine how the error decreases as the method continues.
2. Linear Interpolation Methods. Tells how approximating the function in the vicinity of the root with a straight line can find a root more efficiently. It has a better "rate of convergence".

3

Newton's Method. Explains a still more efficient method that is very widely used but there are pitfalls that you should know about. Complex roots can be found if complex arithmetic is employed.

4

Muller's Method. Approximates the function with a quadratic
polynomial that fits to the function better than a straight line. This significantly improves the rate of convergence over linear interpolation.

5

Fixed-Point Iteration: 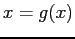$x=g(x)$ Method. Uses a different approach: The function 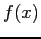$f(x)$ is rearranged to an equivalent form, 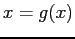$x=g(x)$. A starting value, 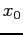$x_0$, is substituted into 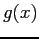$g(x)$ to give a new x-value, 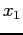$x_1$. This in turn is used to get another x-value. If the function 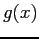$g(x)$ is properly chosen, the successive values converge.