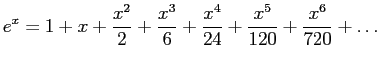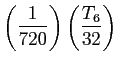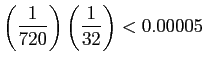Economizing a Power Series
- We begin a search for better power series representations of functions by using Chebyshev polynomials to economize a Maclaurin series.
- This will give a modification of the Maclaurin series that produces a fifth-degree polynomial
- whose errors are only slightly greater than those of a sixth-degree Maclaurin series.
- We start with a Maclaurin series for
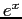 :
:
- If we would like to use a truncated series to approximate
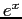 on the interval
on the interval ![$ [0, 1]$](img931.png) with a precision of
with a precision of 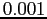 ,
,
- We will have to retain terms through that in
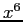 , because the error after the term in
, because the error after the term in 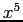 will be more than
will be more than
- Suppose we subtract
from the truncated series.
Table 6.1:
Comparison of economized series with Maclaurin series.
![\begin{table}\begin{center}
\includegraphics[scale=0.8]{figures/4.2.ps}
\end{center}
\end{table}](img942.png) |
- We economize in that we get about the same precision with a lower-degree polynomial.
- By subtracting
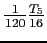 we can economize further, getting a fourth-degree polynomial that is almost as good as the economized fifth-degree one.
we can economize further, getting a fourth-degree polynomial that is almost as good as the economized fifth-degree one.
- So that we have found a fourth-degree power series that meets an error criterion that requires us to use two additional terms of the original Maclaurin series.
- Because of the relative ease with which they can be developed, such economized power series are frequently used for approximations to functions.
- Much more efficient than power series of the same degree obtained by truncating a Taylor or Maclaurin series.
- Observe that even the economized polynomial of degree-4 is more accurate than a fifth-degree Maclaurin series.
- Also notice that near
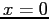 , the economized polynomials are less accurate.
, the economized polynomials are less accurate.
- We can get the economized series with MATLAB by employing our M-file for the Chebyshev series.
- We must start with
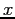 as a symbolic variable, then get the Maclaurin series and subtract the proper multiple of the Chebyshev series:
as a symbolic variable, then get the Maclaurin series and subtract the proper multiple of the Chebyshev series:
Cem Ozdogan
2011-12-27