Fourier Series for Nonperiodic Functions and Half-Range Expansions
Figure 6.8:
A function, 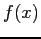 , of interest on [0,3].
, of interest on [0,3].
|
|
Figure 6.9:
Left: Plot of a function reflected about the y-axis, an even function,Right: Plot of a function reflected about the origin, an odd function.
|
|
- The development until now has been for a periodic function. What if
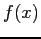 is not periodic? Can we approximate it by a trigonometric series? We assume that we are interested in approximating the function only over a limited interval and we do not care whether the approximation holds outside of that interval.
is not periodic? Can we approximate it by a trigonometric series? We assume that we are interested in approximating the function only over a limited interval and we do not care whether the approximation holds outside of that interval.
- Suppose we have a function defined for all
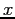 -values, but we are only interested in representing it over (0, L). Figure 6.8 is typical.
-values, but we are only interested in representing it over (0, L). Figure 6.8 is typical.
- Because we will ignore the behavior of the function outside of (0, L), we can redefine the behavior outside that interval as we wish
Figs. 6.9left and -right show two possible redefinitions.
- In the first redefinition, we have reflected the portion of
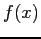 about the
about the 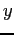 -axis and have extended it as a periodic function of period
-axis and have extended it as a periodic function of period 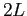 . This creates an even periodic function.
. This creates an even periodic function.
- If we reflect it about the origin and extend it periodically, we create an odd periodic function of period
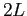 .
.
It is easy to see that 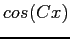 is an even function and that
is an even function and that 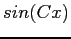 is an odd function for any real value of
is an odd function for any real value of 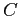 .
.
- There are two important relationships for integrals of even and odd functions.
- the product of two even functions is even;
if 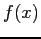 is even,
is even,
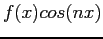 is even
is even
- the product of two odd functions is even;
if 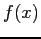 is odd,
is odd,
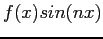 is even
is even
- the product of an even and an odd function is odd;
if 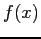 is even,
is even,
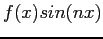 is odd
is odd
if 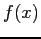 is odd,
is odd,
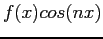 is odd
is odd
- The Fourier series expansion of an even function will contain only cosine terms (all the
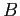 -coefficients are zero).
-coefficients are zero).
- The Fourier series expansion of an odd function will contain only sine terms (all the
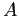 -coefficients are zero).
-coefficients are zero).
- If we want to represent
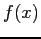 between 0 and
between 0 and 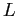 as a Fourier series and are interested only in approximating it on the interval
as a Fourier series and are interested only in approximating it on the interval 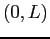 , we can redefine
, we can redefine 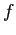 within the interval
within the interval 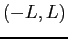 in two importantly different ways;
in two importantly different ways;
- We can redefine the portion from
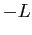 to 0 by reflecting about the
to 0 by reflecting about the 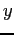 -axis. We then generate an even function.
-axis. We then generate an even function.
- We can reflect the portion between 0 and
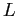 about the origin to generate an odd function.
about the origin to generate an odd function.
Figure 6.10:
Left: Plot of the function reflected about the y-axis, Right: Plot of the function reflected about the origin.
|
|
Figure 6.10 shows these two possibilities.
- Thus two different Fourier series expansions of
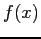 on
on 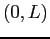 are possible, one that has only cosine terms or one that has only sine terms. We get the
are possible, one that has only cosine terms or one that has only sine terms. We get the  s for the even extension of
s for the even extension of 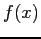 on
on 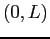 from
from
We get the 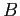 s for the odd extension of
s for the odd extension of 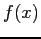 on
on 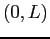 from
from
Examples:
- Find the Fourier cosine series expansion of
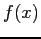 , given that
, given that
Figure 6.10left shows the even extension of the function. Because we are dealing with an even function on 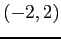 we know that the Fourier
series will have only cosine terms. We get the
we know that the Fourier
series will have only cosine terms. We get the 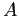 s with
s with
Then the Fourier cosine series is
- Find the Fourier sine series expansion for the same function. Figure 6.10right shows the odd extension of the function.
We know that all of the
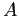 -coefficients will be zero, so we need to compute only the
-coefficients will be zero, so we need to compute only the 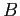 s;
s;
Cem Ozdogan
2011-12-27
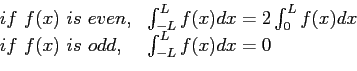
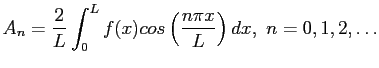
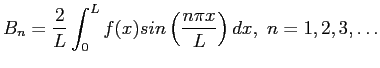
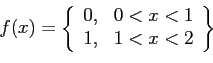
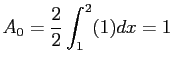
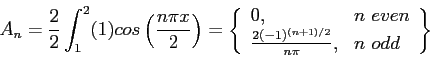
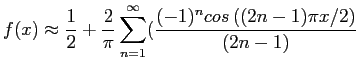
![$\displaystyle B_n=\frac{2}{2}\int_1^2(1)sin(\frac{n\pi x}{2})dx=\frac{2}{n\pi}\left[-cos(n\pi)+cos(\frac{n\pi}{2})\right], n=1,2,3,\ldots
$](img1045.png)
![$\displaystyle f(x)=\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{\left[cos(n\pi /2)-cos(n\pi)\right]}{n}sin(\frac{n\pi x}{2})
$](img1046.png)