Next: Hands-on- Interpolation and Curve Up: week56l Previous: week56l
function [k,X]=jacobi(A,B,P,delta, max1)
% Input - A is an N x N nonsingular matrix
% - B is an N x 1 matrix
% - P is an N x 1 matrix; the initial guess
% - delta is the tolerance for P
% - max1 is the maximum number of iterations
% Output - X is an N x 1 matrix: the jacobi approximation to
% the solution of AX = B
N = length(B);
for k=1:max1
for j=1:N
X(j)=(B(j)-A(j,[1:j-1,j+1:N])*P([1:j-1,j+1:N]))/A(j,j);
end
err=abs(norm(X'-P));
relerr=err/(norm(X)+eps);
P=X';
if (err<delta)|(relerr<delta)
break
end
end
X=X';
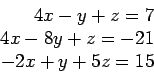
>> A=[4 -1 1; 4 -8 1;-2 1 5] >> B=[7 -21 15]' >> P=[1,2,2] >> [k,X]=jacobi(A,B,P,10^-9,20)