Next: Hypergeometric Distribution Up: Some Discrete Probability Distributions Previous: Discrete Uniform Distribution
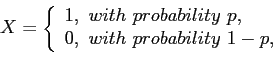

: is the number of sample points that have ![]() successes.
successes.
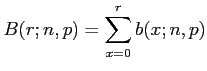
: is the binomial sums.
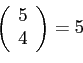 cases of making 4 successes among 5 trials,
cases of making 4 successes among 5 trials,
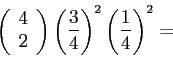
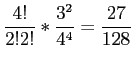
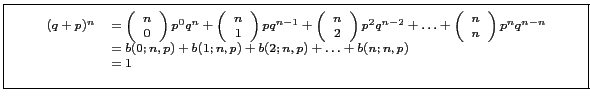
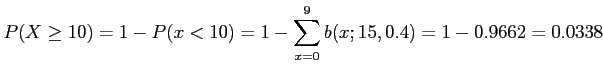
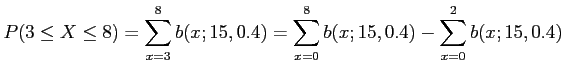
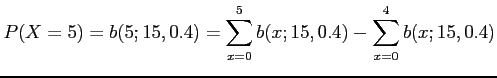
Denote by ![]() the number of defective devices among the 20;
the number of defective devices among the 20;
![]()
Denote by ![]() the number of shipments containing at least one defective item;
the number of shipments containing at least one defective item;
![]()
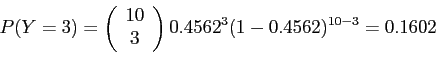

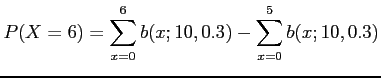
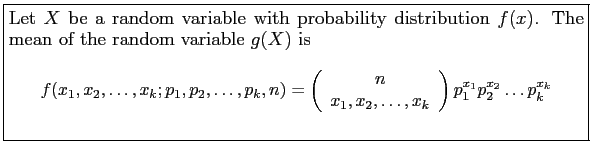
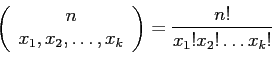
Let ![]() be the number of customers buy
be the number of customers buy ![]() product,
product,
![]() . Then
. Then
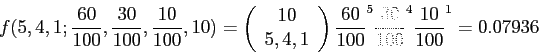
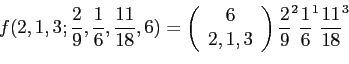
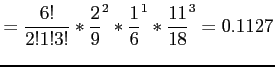
Cem Ozdogan 2010-04-08